Redis的有序集合ZSet

之前写了一篇基于Redis的ZSet的数据类型实现分页查找的，今天咱们聊聊关于ZSet的基本用法和实现原理。

1.Zset基本使用

在日常开发中的话，Spring也提供了Redis的客户端，ZSet的使用来自接口：org.springframework.data.redis.core.ZSetOperations

添加元素

127.0.0.1:6379> zadd mykey 55 test1 66 test2 77 test3    //添加三个元素
(integer) 3

删除元素

 127.0.0.1:6379> zrem mykey test1
 (integer) 1

获取区间元素

    127.0.0.1:6379> zrange mykey 0 -1                        //使用zrange命令可以获取所有元素
    1) "test2"
    2) "test3"

根据score范围获取数据

127.0.0.1:6379> zrangebyscore mykey -inf +inf
1) "test-1"
2) "test1"
3) "test2"
4) "test3"

-inf 和 +inf是负无穷和正无穷，该命令表示获取所有数据

zrangebyscore mykey 0 +inf limit 0 5 //可以结合limit的命令限制返回数据个数

zscan遍历获取数据

127.0.0.1:6379> zscan mykey 0 match test* count 5
1) "2"
2)  1) "test448"
    2) "48"
    3) "test-1"
    4) "-11"
    5) "test3"
    6) "77"
    7) "test52"
    8) "52"
    9) "test53"
   10) "53"

下一次获取得把0换成2去获取下一批数据。
说明一下：当数据量较小时或者不存在数据大于64字节时是一把返回所有数据的。即使设置了count值也是不生效的。

还有一些使用字段序返回，或者使用逆序返回的命令。

2.ZSet原理

ZSet采用了两种不同的结构来实现：

压缩链表(ziplist) 元素个数 <= 128 && 任何一个元素<=64字节高版本已经使用listpack(紧凑列表)

hash + 跳表(skiplist)

ZSet的结构体定义在adlist.h中
typedef struct zset {
  dict *dict;
  zskiplist *zsl;
} zset;

dict结构提供了value和score之间的映射关系；zskiplist就是跳表的结构；

使用链表存储，在查找一个元素时，主要是通过遍历的方式，每个元素比较一次，这样的话效率比较低。为了解决查找元素效率低的问题，前辈们使用跳表的方式来查找，如下图所示：

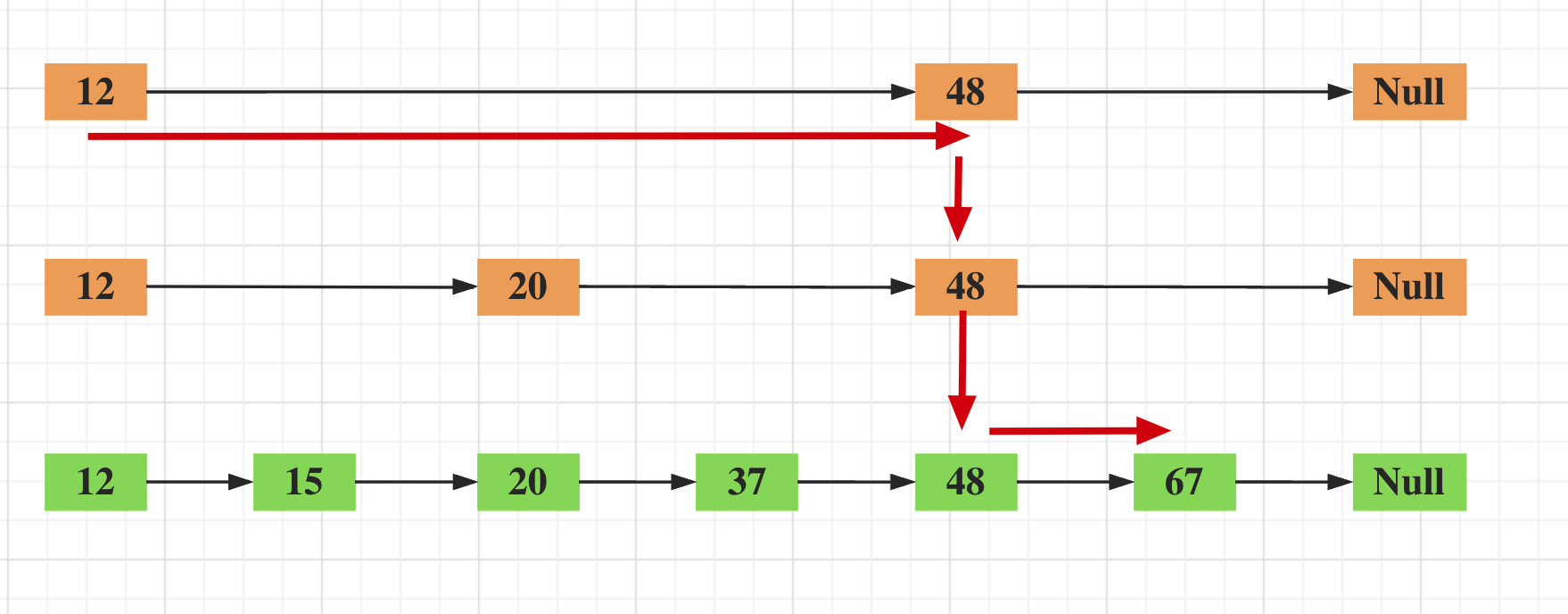
上图中查找67这个元素，首先在第一层找到48位置，然后降到下一层，再降到下一层，往右查找。第一层找到48时候就跳过12到48之间了的元素遍历，很大程度上提高了查找的性能。从整个查找的过程而言和二分查找过程基本类似，因此跳表的查找复杂度也是log(n)。另外上图中的三个链表只是省去了接近一半的元素，提供了一个稀疏的元素，也有人称其为稀疏索引。

那对于48这个元素如何进行降层，然后降到最后一层进行查找呢？接下来看看ZSet在redis中的结构设计。

数据结构定义：

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    sds ele;              //存储value的值
    double score;         //和ele之间存在映射关系，用于对ele进行排序
    struct zskiplistNode *backward;  //最底层节点的前一个节点的指针

    struct zskiplistLevel {
        struct zskiplistNode *forward; // 节点在当前层指向下一个节点的指针
        unsigned long span;  //跨度 该层节点到达下一节点应该要跨越的节点数量 可用于计算排序的名次
    } level[];  //保存每一层指针和跨度
} zskiplistNode;

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;  //头结点 尾结点
    unsigned long length;  //长度
    int level;   //跳表的层数，每次都会从最高层查找的
} zskiplist;

将每一层的节点构建了相应的关系，这时就会可以使用降级的方式实现查找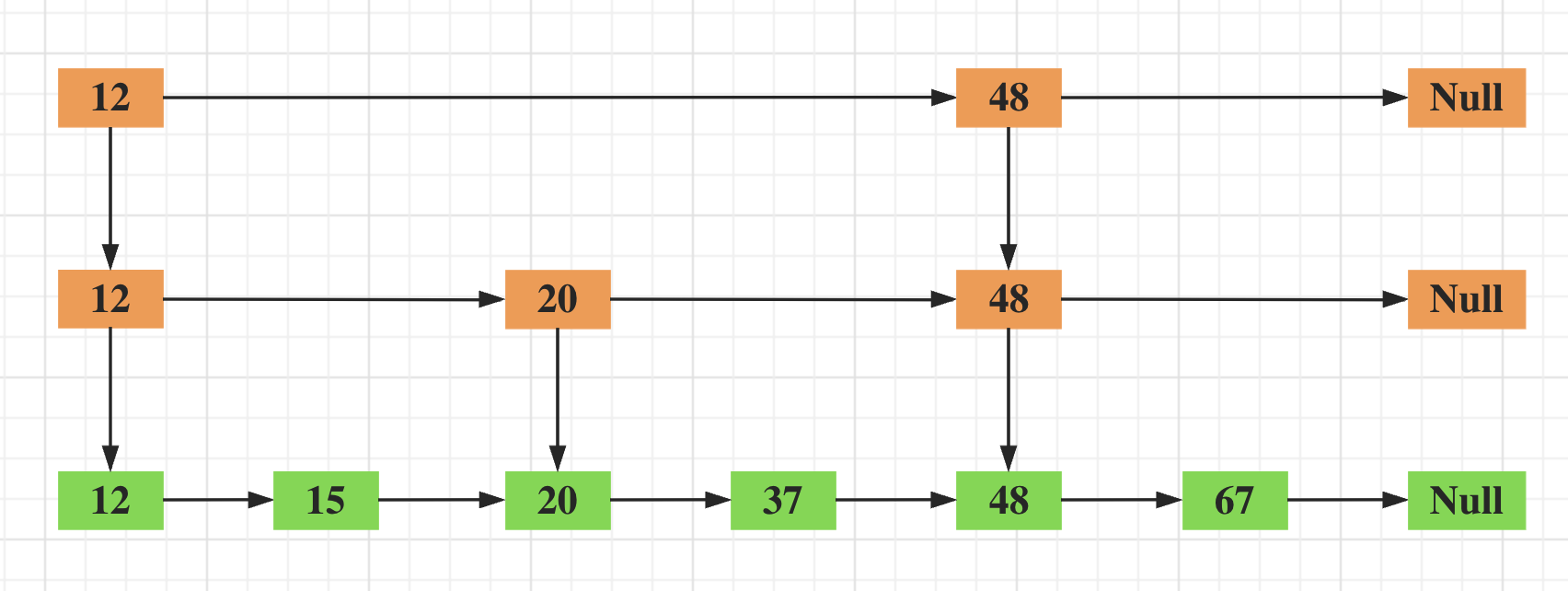：由上述的图和跳表的数据结构比较难想象其对应关系，对于下述的结构和跳表的结构很容易联系之间的关系。

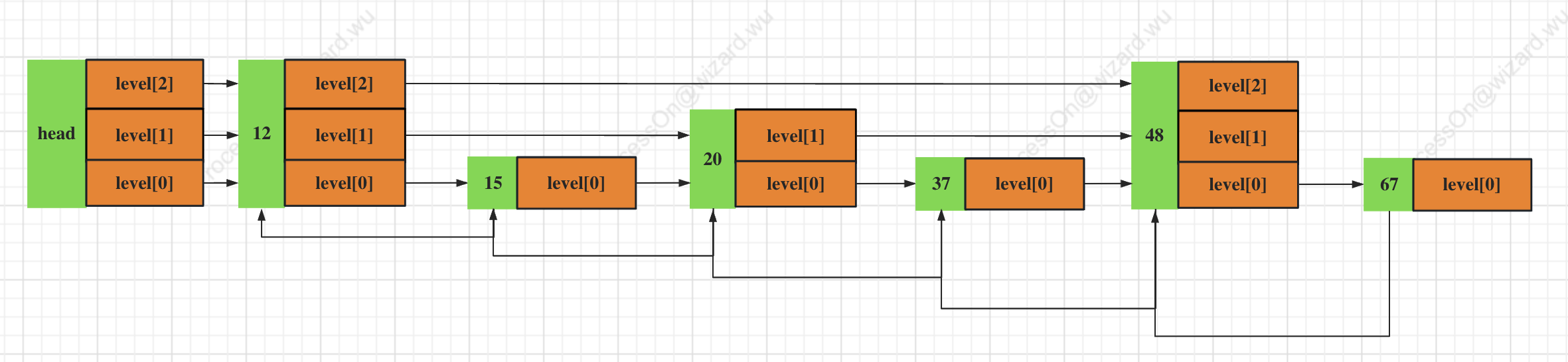
以元素48这个节点为例子：

ele = 48， score = 48(在图中没有显示)

backward = 元素37的地址

level[2] = {forward: null, span:3}

level[1] = {forward: null, span:1}

level[0] = {forward: 67, span:0}

以元素12这个节点为例：

ele = 12， score = 0(在图中没有显示)

backward = 元素null的地址

level[2] = {forward: 48, span:0}

level[1] = {forward: 20, span:0}

level[0] = {forward: 15, span:0}

Redis 跳跃表默认允许最大的层数是 32，被源码中 ZSKIPLIST_MAXLEVEL 定义，当 Level[0] 有 2^64 个元素时，才能达到 32 层，所以定义 32 完全够用了。

2.1插入数据

ZSet在插入一条数据时主要步骤：

(a).寻找插入的位置；

(b).生成随机的层数；

(c).创建插入数据节点；

(d).更新level层的前节点指向当前新增的节点；

(e)更新level[0]层的后节点；

通过源码具体看看每一步的细节, 源码来自t_zset.c的方法zslInsert：

   //(a)寻找插入的位置
   //1.从最高层开始，知道0层
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        //如果score小于直接往右边找；
        //如果scode相等的话 要根据字典顺序排序查找 满足的条件往右边找
        //不满足结束while循环 开启for的新一轮循环 level降一级
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            //同一层满足条件就会往下一个节点 同时存储rank，后期用于span值
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        //这个数组很重要，存储了节点的查询过程，并且对新增节点的替换过程很重要
        update[i] = x;
    }

    //(b) 生成随机层数
    level = zslRandomLevel();
    //如果生成出来的层数大于当前所有节点的层数 要更新新增的层数地址
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;   //将头结点赋值给update新的level层 后期可以直接将zsl->header指向新节点
            update[i]->level[i].span = zsl->length;   //更新长度
        }
        //更新最大层数
        zsl->level = level;
    }

//为节点生成一个level数量
int zslRandomLevel(void) {
    static const int threshold = ZSKIPLIST_P*RAND_MAX; //ZSKIPLIST_P 为0.25
    int level = 1;
    while (random() < threshold)
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL; //不超过32的限制
}

#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^64 elements */

跳表在创建节点时候，会生成一个范围在 0~1 的随机数，如果这个随机数小于 0.25（相当于概率 25%），那么层数就增加 1 层；然后继续生成下一个随机数，直到随机数的结果大于 0.25 结束，最终确定该节点的层数。这样的做法，相当于每增加一层的概率不超过 25%，层数越高，概率越低.

    //(c).创建插入数据节点
    x = zsljavareateNode(level,score,ele);
    //(d).更新level层的前节点指向当前新增的节点
    for (i = 0; i < level; i++) {
        //为新创建的节点的前驱节点赋值 和链表插入一样
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        //为当前节点生成span值
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }
   //(e).更新level[0]层的后节点
   x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;

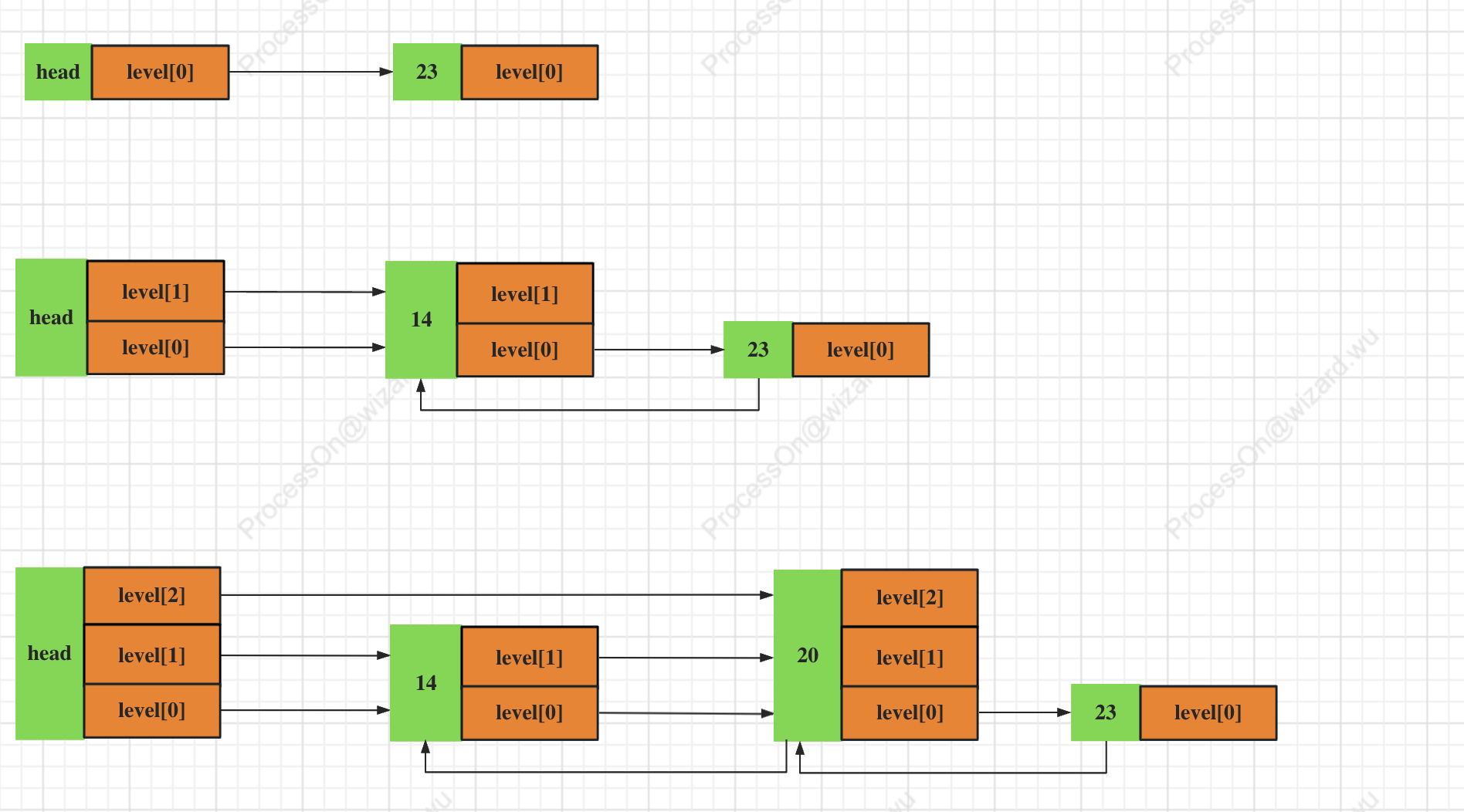
对于第三层新增的20这个节点时，根据程序：

首先找到14这个节点位置，update[1] = 14, update[0] = 14.

这时候生成层高为3，zsl->level = 3, update[2] = zsl->head

创建20的节点x: 进行替换操作

x->level[0].forward = update[0] ->level[0].forward. 相当于把14的前驱节点23 赋给了20这个前驱节点；

update[0]->level[0].forward = x, 把20这个节点赋给了14的前驱节点

这是第一层的插入过程，其他层依次类推。

对于第三层之前存在的上述update[2] = zsl -> head.

因此此时 x->level[2].forward = update[2]->level[2].forward, 对于 update[2]->level[0].forward是新创建的层数，所以为null。

update[2]->level[2].forward 指向了x节点。

最后更新底层后驱节点，因为后驱节点只有level[0]存在，所以只需要对level[0]进行更新。

2.2删除节点数据

源码来源： t_zset.c/zslDeleteNode

删除节点数据步骤：

(a).找到删除的位置；

(b).如果删除节点是最高的level，更新ZSet的level；

(c).长度减一；

(d).删除成功返回1，没有该节点返回0；

2.3 更新节点数据

更新数据主要是更新score的值，对于使用zadd插入数据时，如果value不同会插入，如果相同就更新。上文提到了dict的结构，该结构维护了value和score的映射关系，所以小编最初理解时只需要找到value的score进行更新就可以了，实际上更新完了score就不满足有序性了。

更新节点数据步骤：

a).找到节点的位置；

b).节点新的score更新后不影响位置的改变，直接用新的score替换即可；

c).如果不满足步骤b，先删除节点；

d).以新的score来新增这个节点；

2.4节点数据获取

通过下图的一个案例来描述Zset整个查找数据的过程，下图是需要寻找37 这个节点:

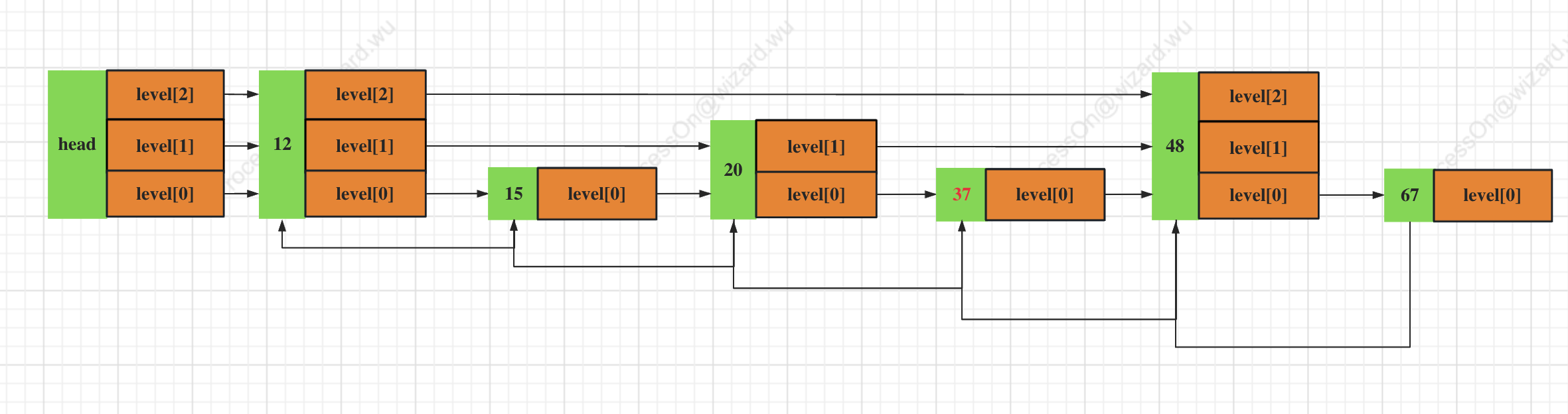
从顶层level[2]开始, ZSet中存储了level的最大值head.level[2].forward，这个值是12；
12 < 37, 则比较12.level[2].forward, 这个值是48；
48 > 37, 则进行for循环 level层数减一, 即12.level[1].forward, 这个值是20；
20 < 37, 则比较20.level[1].forward, 这个值是48；
48 > 37, 则进行for循环level层减一，即20.level[0].forward, 这个值是37；
37 == 37，返回数据；

2.5批量数据获取

批量获取数据时是需要一个起始点的，例如使用zrangebyscore mykey 0 +inf limit 0 5 命令返回数据时，最先时通过获取score为0的元素，如果没有就是从大于0的第一个元素开始，获取5个元素并返回。

整个流程也是需要先知道score为0的节点，以score为0的节点为中心，往左边数5个就是反序返回，往右边数5个就是正序返回。

3. 总结

本文主要讲述ZSet的基本使用命令和增删改查的基本原理，并结合源码对增加节点的过程进行了深入介绍。说明了ZSet是一种稀疏索引结构，并不是严格意义的二叉树，只能说是一种趋势上的二叉树，主要是通过随机次数来决定节点的层高的。

总结一个高频面试题：为什么ZSet采用这个跳表而不是红黑树的数据结构？

先贴上作者解释链接

There are a few reasons:

They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.

A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.

They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

作者从三个角度解释：

内存占用: 作者认为使用跳表对于节点的存储占用内存更少，红黑树需要左右两个子树的指针存储，跳表中的指针数量取决于随机数中的0.25，根据计算公式E = 1 + p*(1 + p + p^2 + p^3 + ... + p^(k-1)), 平均下来1.33个指针存储。
范围查找: 上述根据批量数据获取的时候说明了，其实和B+树对于B树的优化一样，支持了范围查找。
算法实现: 实现起来比红黑树简单。

实际上对于红黑树的插入和删除操作时是有性能损耗的，红黑树为了保持自身的平衡，每次插入和删除都要检查是否平衡，不平衡需要通过变色和左旋右旋来实现平衡。

PREVIOUSSpringBoot整合Redis集群模式

NEXTKafka分析与总结